【中間テスト終了】国語９０点!学年１位!「こんな点数取ったことないし!!」
まもなく、中間テストを迎える、高校1年生のアナタに。数学Aの場合の数・順列で苦しんでいるアナタに。
今回は数学Aの中間テストでよく出る、サイコロ問題のすごく簡単に答えが出せる必殺技の一つをお教えします。
「場合の数」は、問題ごとに解答方法に慣れなければいけない
数学A「場合の数」の単元で必要なのは、文章で示された「現場」を理解し、該当事象をもれなく数え上げることです。従って、複雑な計算は必要ありません。算数のセンスがよい小学生４年生でも、解答できる子が出てくるでしょう。
しかし、学校の教科書や問題集に登場する問題は、それぞれの問題ごとに、典型的な考え方と解き方を知っておく必要があります。解き方を知らない問題は、全く手が出せずに困ると思います。
場合の数の基本は「もれなく数え上げ」ること!!
教科書に載っていた問題を一つ、例に挙げて説明します。
【問題】大小２つのサイコロを投げるときに、目の和が５の倍数になる場合は何通りあるか。
【教科書の解答】
(i)目の和が5になるのは (1,4)(2,3)(3,2)(4,1) の４通り
(ii)目の和が10になるのは (4,6)(5,5)(6,4) の3通り
和の法則により、4+3=７通り
この解法では、うっかりミスでモレが生じたり、重複が生じたりすると、不正解になります。
単純ミスで悔しい思いをする人は少なくありません。
この方法を中学で習っている人もいるかもしれませんが、こんな表を書いてみてください。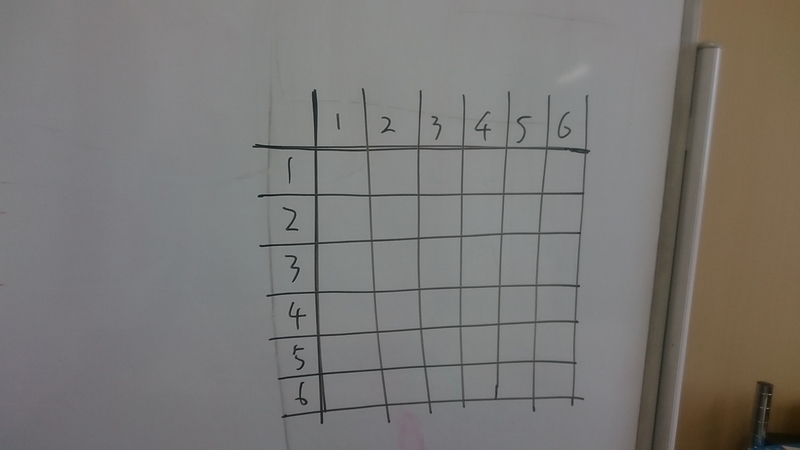
マス目の分だけサイコロの出目があります。
そして、該当する部分だけ、マルをつけて数え上げてしまいましょう。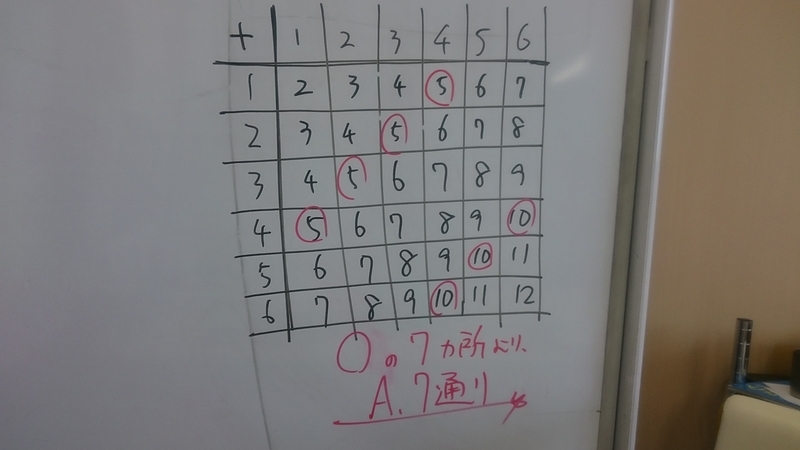
該当するパターンを、もれなく、正確に、すべて数え上げることが、「場合の数」の極意です。
「サイコロ２つ」問題は、表を書けばいい!!
実は「サイコロ２つを使って・・・」と書かれている問題は、このサイコロ表を書いて数え上げてしまえば、どんな問題でも解けてしまいます。ホントにどんな問題でも、解けてしまいます!!
このことについては、次のコラムにまとめてみます。
ご期待ください。
