第45回 不常識を非まじめに考えた小学生の特許(米国編)
このコラムの第10回で、発明は天才のひらめきによるものではなく、だれでも発明可能であることを既に説明した。そして、第41回~第47回では、幼児や小学生の発明した特許を紹介した。今回からは主婦の発明力や考案力等を紹介していく予定である。
今回のコラムでは、前半の§1~§3で人類の二千五百年以上に渡る大問題に挑戦し、専門家を驚かした米国の主婦の研究を紹介する。後半の§4~§5では、実用新案権のロイヤリティーで6000万円以上の収入を得た日本の主婦の知的財産権を生かした事業展開を説明する。
以下の説明から発明・考案や創作には、その人の過去の経歴や専門性は関係ないことを理解していただければ幸いである。恩師西沢潤一先生は、「誰でも1年間一生懸命努力すれば専門家になれる」と、ご指導されていた。
§1 人類が二千五百年以上に渡って取り組んできた大問題
§2 専業主婦の興味が人類の大問題に挑戦
§3 平面充填の研究から派生したノーベル賞
§4 ロイヤリティーで6000万円以上の収入を得た主婦
§5 主婦であっても連続的に複数の権利を獲得する
§1 人類が二千五百年以上に渡って取り組んできた大問題
「どのような形状の凸多角形であれば、固定された一種類の形状のタイルで平面を充填することができるか」というのは、古代ギリシア時代から数学の専門家を魅了してきた問題である。
紀元前5~6世紀のピタゴラス学派が、一種類のタイルで平面を平行移動と反転だけで隙間が出来ないように平面充填することができる正多角形の形状は,正三角形、正方形、正六角形の三種類のみであることを証明している。しかし、正多角形という条件を外すと五角形でも平面充填が可能である。
平面充填が可能な凸多角形の平面形状はどのくらいあるかという問題は、二千五百年以上に渡る数学の謎になっていた。1900年にパリで開催された国際数学者会議でドイツのゲッティンゲン大学のダフィット・ヒルベルト(David Hilbert)教授が、当時の数学界の残っている未解決問題が23あるというリストを挙げた。
ヒルベルト教授のリストの18番目が「結晶群・平面充填・最密充填」の問題であった。ヒルベルト教授は、アルベルト・アインシュタイン(Albert Einstein)より先に、一般相対性理論の重力方程式を投稿していた数学界の大御所で「現代数学の父」とも呼ばれている。
K.A.ラインハルト(Reinhardt)氏が、1918年に彼の博士論文で凸六角形の場合は正六角形以外には3タイプしか平面充填できないことを証明した。後にK.A.ラインハルト博士はヒルベルト教授の助手を経てフランクフルト大学の教授となった。1918年の博士論文で、K.A.ラインハルト教授は、凸五角形では5つのタイプを発見したが、それ以外の平面充填可能な凸五角形が存在するか否かは、K.A.ラインハルト教授には分からなかった。
表1に示すように、K.A.ラインハルト教授がタイプ1~5の凸五角形を発表してから50年後の1968年、R.B.カーシュナー(Kershner)教授が新凸五角形を3つ発見し、他に平面充填可能な凸五角形はないと主張した。
【表1】平面充填可能な凸五角形の研究の歴史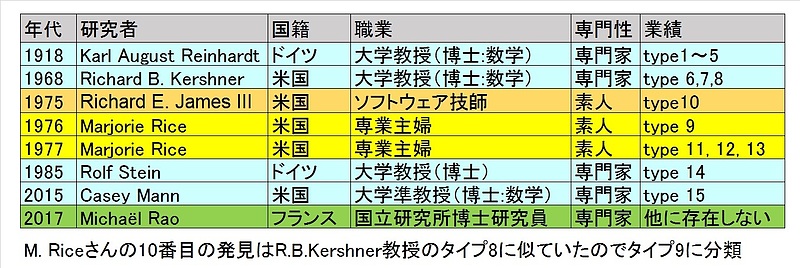
そして、1975年7月、米国の数学者M.ガードナー(Gardner)氏が、サイエンティフィック・アメリカン(Scientific American)に1957年から連載している自身の「数学ゲーム(Mathematical Games)」のコラムで凸五角形による平面充填の問題を取り上げた(Martin Gardner, "On tessellating the plane with convex polygon tiles ", Scientific American, Vol. 233, No. 1, (1975), pp. 112-117)。
「カーシュナーにより3つの凸五角形が発見されたが、カーシュナーの論文に、平面を埋め尽くす他の凸五角形はないとの証明はない」とガードナー氏は書いている。
§2 専業主婦の興味が人類の大問題に挑戦
米国カリフォルニア州サンディエゴ市で5人の子供を育てている52歳の主婦マジョリー・ライス(Marjorie Rice)さんは、中学生の息子のデイビッド(David)君が定期購読している雑誌「サイエンティフィック・アメリカン(Scientific American)」の1975年7月号で、「平面充填可能な5角形はまだ他にあるでしょうか?」というガードナー氏のコラムを読んだ。
更に1975年12月のガードナー氏のコラムには、一般読者であるソフトウェア技師のR.E.ジェイムス(James)氏から9番目の凸五角形を発見した報告があったことが記載された。
(Martin Gardner, "A random assortment of puzzles, together with reader responses to earlier problems”, Scientific American, Vol. 233, No. 6, (1975), pp. 116-119)
高校で数学を一年しか勉強せず、すぐに就職し、その後専業主婦になってしまったのにも関わらず、パズル好きのマジョリーさんは「おもしろそう!」と興味を持ったそうである。
そして、凸五角形の平面充填に必要な条件を見つける理論構成を、独自に考案して、子供を学校に送り出した後、マジョリーさんは家事の合間に研究を開始した。凸五角形の平面充填を検討するためにマジョリーさんが考案した手法は、以下のシャットシュナイダー教授の論文に記載されている:
https://doi.org/10.1080/17513472.2018.1453740
マジョリーさんの家族は、しばしばマジョリーさんが台所でひそかにスケッチしているのを見ている。マジョリーさんの娘、キャシー(Kathy)さんは、「マジョリーさんが落書きしていると思った」そうである。
第10回で、エジソンの発明の手法を紹介したが、マジョリーさんは独自に考案した手法で過去の平面充填可能な凸五角形について、エジソンと同様に分析と検討を重ねた。そして、1976年の2月までにマジョリーさんは平面充填可能な新凸五角形を発見し、サイエンティフィック・アメリカンのガードナー氏に報告する。
ガードナー氏は、ペンシルベニア州モラヴィアン大学(Moravian College)で凸五角形の平面充填を研究している数学科の教授のD. J.シャットシュナイダー(Schattschneider)博士に検証を依頼した。
マジョリーさんが10番目に発見した新凸五角形は1968年にR.B,カーシュナー教授が発見したタイプ8に似ていたのでタイプ9に分類された。1975年にR.E.ジェイムス氏が発見した9番目の凸五角形がタイプ10に分類された。
シャットシュナイダー教授の指導を受けながら、マジョリーさんは更にタイプ11-13の新凸五角形を発見した。サイエンティフィック・アメリカンの記事を読んだ1975年からわずか2年という短期間に、図1に示すように、全部で4種類の平面充填可能な新凸五角形を、家庭の専業主婦が発見したのである。
【図1】マジョリー・ライスさんが発見した4つの新凸五角形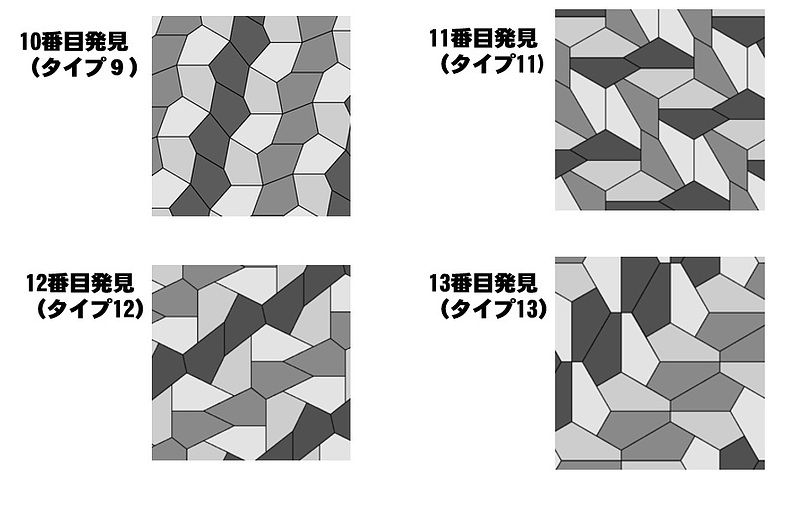
その後1985年になって、R.シュタイン(Stein)教授が14番目の凸五角形(タイプ14)を発見する。それから、更に30年後の2015年にC.マン(Mann)准教授が15番目の平面充填可能な凸五角形(タイプ15)を発見した。
マジョリーさんは、2017年7月に94歳で亡くなった。2017年8月になり、コンピュータ支援の新証明法で、フランスの数学者 M.ラオ(Rao)博士 が、15種類(15タイプ)の凸五角形が存在するのが正しく、15種類以外には平面充填可能な凸五角形は存在しないと主張した。ただし、M.ラオ博士の主張はまだ他の研究者により検証されていないようである。
Michael Rao,”Exhaustive search of convex pentagons which tile the plane”
http://perso.ens-lyon.fr/michael.rao/publi.php?lang=en
人類の長年の課題であった凸五角形の平面充填の物語がついに完結した可能性があることを、マジョリーさんは知ることはなかった。タイプ10の凸五角形を発見したR.E.ジェイムス氏も数学の専門家ではない。よって、全部で15の凸五角形の内の1/3を占める5つの平面充填可能な凸五角形が、数学の素人によって発見されているのである。
§3 平面充填の研究から派生したノーベル賞
冒頭で述べたとおり、ピタゴラス学派が、平面充填可能な正多角形は正三角形、正方形、正六角形の三種類しかないことを証明した。同様に、原子、分子やイオンが構成する結晶が3次元空間での充填のし方の回転対称性も、3回対称・4回対称・6回対称の3通りしかない。ヒルベルト教授が18番目の問題として、「結晶群・平面充填・最密充填」を挙げたのもこのような事情からである。
正五角形では隙間が空いてしまい平面充填ができないので、5回対称の対称性は、平面充填とは相性が悪いと思われていた。しかし、オックスフォード大学のロジャー・ペンローズ(Roger Penrose)教授が、2種類の菱形から成るタイルパターンで、5回対称の対称性を持ち、しかも周期性を持たない平面充填のパターンであるペンローズ・タイルを、1972年に発見した。
そして、ペンローズ・タイルの形式で3次元充填をした「準結晶」を、テクニオン工科大学のダニエル・シェヒトマン(Daniel Shechtman)教授が1984年に発見した。「準結晶」は、「結晶」でも「アモルファス(非結晶)」でもない幾何学的な構造である。準結晶の構造は熱的に不安定であり、通常は時間の経過とともに熱的に安定した結晶の構造になる。2011年になり、シェヒトマン教授はノーベル化学賞を受賞している。
§4 ロイヤリティーで6000万円以上の収入を得た主婦
さて、ここからは日本の横浜市金沢区の主婦鹿島よし子さんの「鍋蓋」の実用新案登録の話を説明する。米国の主婦は一定の形状の凸五角形を敷き詰める問題を研究したが、日本の主婦はどのような大きさの鍋であっても「落し蓋」を敷き詰めることができる器具を研究した。
落し蓋は、日本料理の固有の料理法に用いられる器具である。フランス料理では魚を煮るときに沸騰させていけないとされているので、低温で2時間くらいの時間が必要であるが、落し蓋を用いる日本料理では高温で沸騰させて数分で料理でき、魚のおいしさを生かすことができる。
既にこのコラムの第3回で説明したとおり、平成5年(1993年)の法改正により、平成6年(1994年)の施行から我が国の実用新案は、方式要件などの基礎的要件を判断するのみで早期に登録を行う無審査登録主義を採用している。
後述する表2に示したように鹿島さんは、全部で4つのフリー-サイズ落とし蓋の実用新案権を獲得している。今回、図2を用いて説明する考案は、4つのうちの2番目のフリーサイズ落とし蓋の考案である。
2番目の考案である「鍋蓋」の実用新案登録は、昭和61年(1986年)2月5日に出願し、平成4年(1992年)6月15日に特許庁の審査官による審査を経て公告(特公平4-25073号)された権利であり、公告まで約6年以上を要している。
図2の考案は、昭和51年(1976年)11月24日に出願した基本考案を改良した、改良考案である。
基本考案の出願の方は、昭和55年(1980年)2月18日に特許庁の審査官による審査を経て公告(特公昭55-72153号)されているが、昭和51年の基本考案の方は公告まで約3年以上の時間を要している。
鹿島さんの基本考案も改良考案も、公告までに時間がかかっているが、審査主義の時代に特許庁により「お墨付き」を得た実用新案登録であるので、現在の無審査主義の時代の技術内容に関する「お墨付き」がない実用新案登録とは価値が異なる。
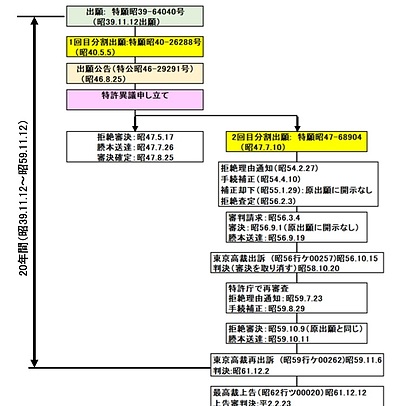
【図2】審査主義の時代の特公平4-25073号に記載されたフリーサイズ落し蓋の構造[ 出典:J-PlatPat]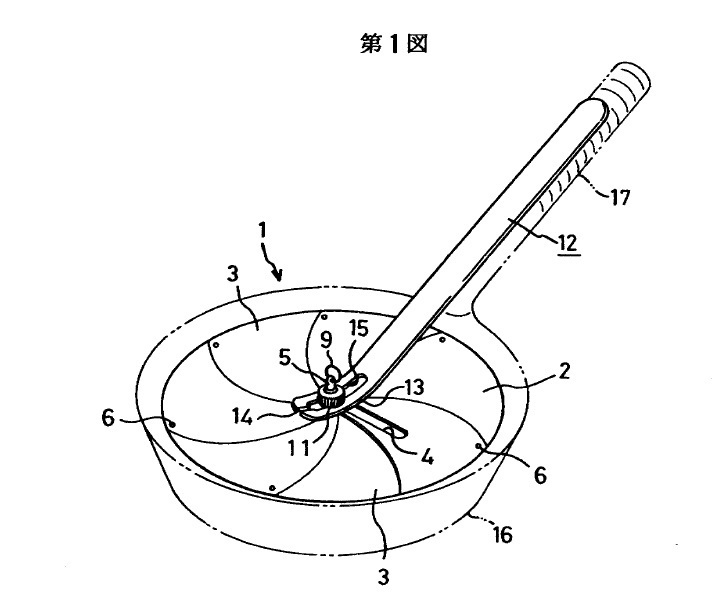
現在の実用新案法第29条の2には、「実用新案権者又は専用実施権者は、その登録実用新案に係る実用新案技術評価書を提示して警告をした後でなければ、自己の実用新案権又は専用実施権の侵害者等に対し、その権利を行使することができない」と規定されている。特許庁の「お墨付き」がない権利であるからである。
平成6年以降に出願された実用新案権は、図2に示した鹿島さんの実用新案登録第1955670号とは異なり、そのままでは権利を行使することができない紙切れに過ぎず、ライセンス交渉に行っても、先方から相手にされないので注意が必要である。
一方、鹿島さんが権利化に成功したフリーサイズ落し蓋は、これまでに800万枚、総額およそ72億円を売り上げているそうである。現在の実用新案権とは異なり、権利を行使することができる知的財産権であり、ライセンス交渉も可能である。
ライセンス契約に伴い、鹿島さんは、実用新案権のライセンス契約のロイヤリティーで6000万円以上の収入を上げることができたということである。契約金が30万円、実施料は3%ということだったらしい。
落し蓋には沸騰した煮汁が蓋に当たり、少ない煮汁でもむらなく煮含める役割があるが、鍋のサイズに合わない落し蓋で調理すると、魚が煮崩れしてしまう。鍋のサイズはいろいろでそれに合わせて落し蓋のサイズ違いも用意するのは大変である。
鹿島さんの落し蓋の理想的なサイズは、鍋の直径よりも、ほんの一回り小さいサイズである。鹿島さんは試行錯誤を繰り返した結果、「大きい蓋を小さくたたむことでサイズを調整する」という方法を考えた。
鹿島さんの落し蓋の構造は、図2に示すように、金属の扇形板3,3…が交互に組まれていて、それが重なり合うことで自由にサイズを変えることができ、あらゆる大きさの鍋に自在に対応できる仕組みになっている。これらの扇形板3は順次重ね合せられた上で各扇形板3の長溝4を貫通するようにボルト5が挿通され、さらに上下方向において隣接する一対の扇形板3,3の上位の一隅部と下位の他隅部とがリベツト6により回転移動できるようになっている。
落し蓋の役割は、煮物が煮汁の中で動き回って煮崩れてしまうのを、金属の扇形板3,3…で材料を軽く抑えることで防ぎ、ぐつぐつと沸いている煮汁をうまく循環させ、少ない煮汁でも効率的に味をしみこませることができる。扇形板3,3…の重なり合いを調整することで、煮汁の急激な蒸発も抑えられ、熱効率の観点から経済的となる。さらに、素材の匂いがこもったりするのを防ぐ効果もある。
§5 主婦であっても連続的に複数の権利を獲得する
鹿島さんの知財戦略の優れている点は、表2に示すように連続的に複数の知財権を獲得している点である。
表2の最初の行(レコード)に記載したのが鹿島さんの基本考案の実用新案登録第1346201号(実公昭55-7215)であり、表2の6番目の行になる黄色のセル記載した考案は、基本考案に柄を付けて構造を改良した改良考案の実用新案登録第1955670号(実公平4-25073)である。
【表2】鹿島さんの連続的知財戦略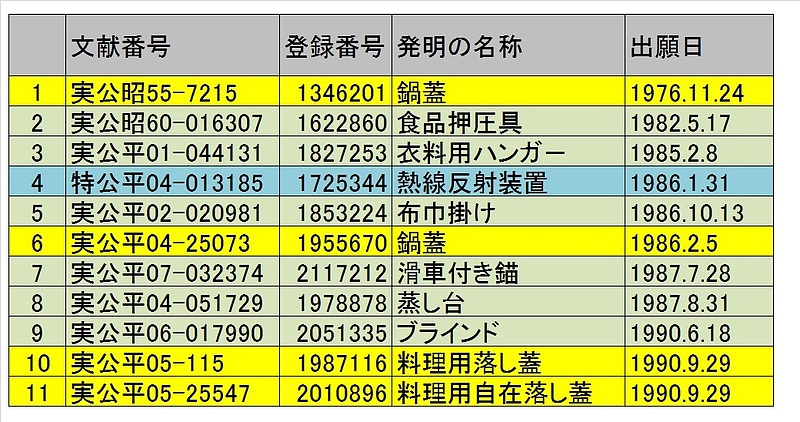
表2の10番目及び11番目の黄色のセルは、鹿島さんの更なる改良考案である。10番目及び11番目の改良考案では、洗浄や消毒が容易な構造に改良されるとともに、扇形板の周辺に穴が空けられている。この多数の穴によって、煮汁がより効率よく循環して、煮物に程よい圧力がかかり味がしみ込みやすい構造に改良されている。
一つ権利化すると安心してしまう発明者や考案者がいるが、知的財産権は連続的に複数を獲得して、複数の権利のマトリクスで保護しなければ、自社の事業を保護できない。
基本考案の実用新案登録第346201号は、1980年(昭和55年)2月18日から1990年2月18日まで10年間の保護期間が与えられた。しかし、鹿島さんは図3に緑色のバーで示すように、改良考案を連続的に出願し、権利化していくことにより約23年間の独占期間を実現したのである。
【図3】1件の保護期間が10年でも、連続的な出願をすることにより20年以上の独占的支配が可能になる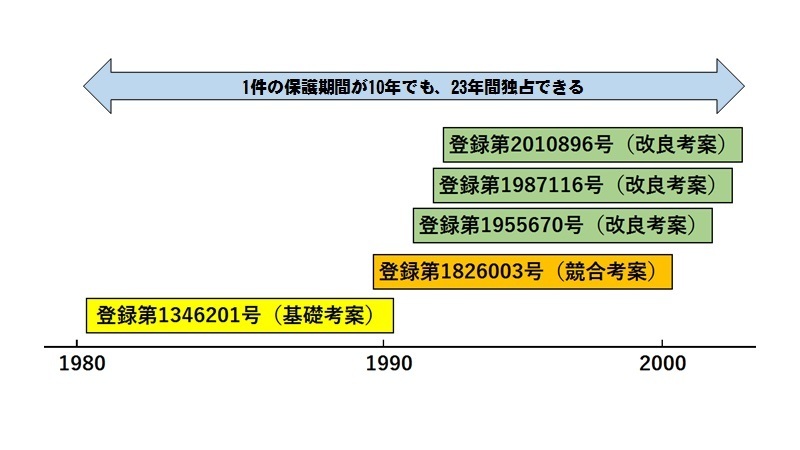
当時は昭和34年法による実用新案法であったので、実用新案権の存続期間は、出願公告の日から10年であったが、実用新案登録出願の日から15年をこえることができなかった(実用新案法第15条)。
このため、鹿島さんの第1改良考案の実用新案登録第1955670号は審査に時間がかかったので、公告日平成4年(1992年)6月15日から10年後の2002年6月15日までではなく、出願日昭和61年(1986年)2月5日から15年後の2001年2月5日までが保護期間となった。
第2改良考案の実用新案登録第2010896号は、1993年6月28日から2003年6月28日までの10年間の保護期間が与えられ、第3改良考案の実用新案登録第1987116号は、1993年1月5日から2003年1月5日までの10年間の保護期間が与えられている。
第2改良考案と第3改良考案は、フリーサイズ落し蓋を販売している下村工業株式会社との共同出願の形式になっている。新潟県三条市にある下村工業株式会社は、独自のOEMシステムを構築して、製品企画から具体的な製品製造を行い、種々の製品を製造している。
第50回で説明したとおり、よい発明や考案は必ず真似をされ、或いは迂回発明や改良発明が現れる。そして、模倣や改良発明をした後発業者の方が、利益を得る場合も多いのである。表2に示した連続的に知的財産権を獲得している鹿島さんの知財戦略を見習う必要がある。
図3で注意して欲しいのは、競合する考案として、長野県上田市の横関正明さんが出願した実用新案登録出願が、オレンジ色のバーで示したように、実用新案登録第1826003号として権利化され、1990年1月5日から2000年1月5日まで10年間の保護期間が与えられていることである。
もし、緑色のバーで示した第1改良考案~第3改良考案の連続的な権利化がなければ、基本考案の存続期間の満了した1990年2月18日年以降は、オレンジ色のバーで示した横関正明さんに市場を独占される可能性があったのである。
辨理士・技術コンサルタント(工学博士 IEEE Life member)鈴木壯兵衞でした。
そうべえ国際実用新案事務所は、種々の創作活動のご相談にも積極的にお手伝いします。
http://www.soh-vehe.jp