幾何公差について

　製品・部品加工に関係する生産技術者として知っておくべき設計図面における幾何公差（geometrical tolerance）について、コメントします。

　幾何公差とは、物体の形状・姿勢・位置関係などの誤差の許容値を表します。設計図面で指示された形状などに加工しようとしても、完全に正しい状態（幾何学的に正しい直線・円・平面）に仕上げることはできません。そこで、どの程度まで歪みやズレを許容できるかを数値化したものとして幾何公差を用います。

　幾何公差は、とある物体の形状の幾何学的な精度を表す指標のことで、わかりやすく説明すると、設計で意図している形状・姿勢・位置関係などの歪みやズレの許容値を意味します。似た単語として「寸法公差」がありますが、寸法公差は図面で記述されている寸法の許容誤差範囲を示しています。寸法公差だけ指示した場合、設計者の意図する正しい形状には指示しきれないため、幾何公差を用いる必要があります。

　幾何公差には、大きく分けて「単独形体」と「関連形体」があります。これらをさらに細かく分類すると、「形状公差」「姿勢公差」「位置公差」「振れ公差」の4つに分かれます。
　●単独形体：形状公差
　●関連形体：姿勢公差・位置公差・振れ公差
　単独形体とは、形状に対して、単独で指定できる幾何公差のことです。幾何公差の分類の「形状公差」が単独形体に該当します。
　関連形体とは、何か基準となる相手との関係を示す必要がある幾何公差のことです。「姿勢公差・位置公差・振れ公差」の3種類が関連形体に該当します。

☆単独形体である形状公差は、以下の6つの特性があります。
　●単独形体（形状公差）：真直度、平面度、真円度、円筒度、線の輪郭度、面の輪郭度

☆関連形体である姿勢公差・位置公差・振れ公差は、それぞれで以下の特性があります。
　●関連形体（姿勢公差）：平行度、直角度、傾斜度、線の輪郭度、面の輪郭度
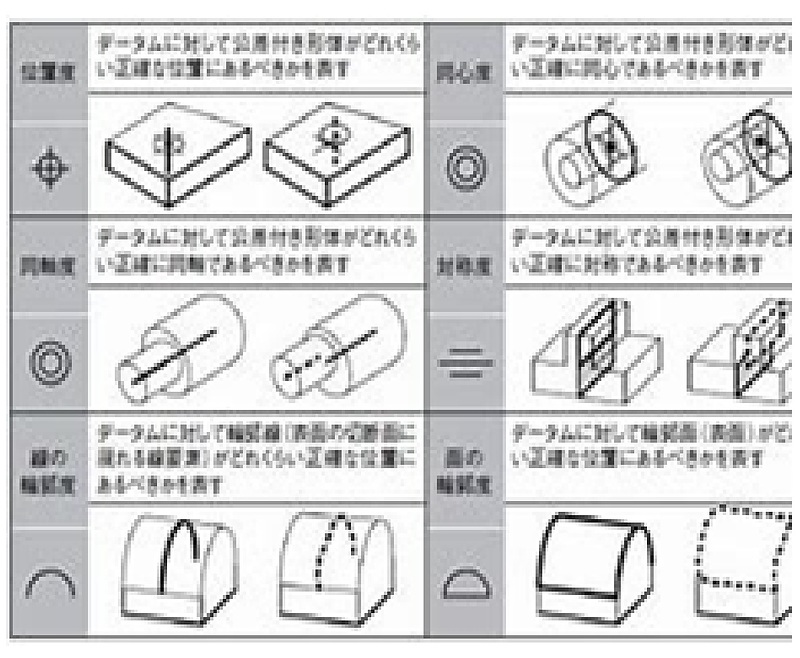
　●関連形体（位置公差）：位置度、同軸度、同芯度、対称度、線の輪郭度、面の輪郭度
　●関連形体（振れ公差）：円周振れ、全振れ

まず、単独形体の各特性についての意味はそれぞれ下記のようになります。
・真直度；指定面や軸が、どれだけ変形しているかを表す幾何公差。
・平面度；平面からどれだけ変形しているかを表す幾何公差。
・真円度；真円からどれだけ変形しているかを表す幾何公差。
・円筒度；円筒状のものが、どれだけ真っ直ぐかつ、丸いかを表す幾何公差。
・線の輪郭度；母線形状がどれだけ変形しているかを表す幾何公差。
・面の輪郭度；線の輪郭度のような二次元の線ではなく、表面形状からどれだけ変形しているかを表す幾何公差。

一方、関連形体の各特性についての意味は下記のようになります。
・平行度；データム直線またはデータム平面に対して、どれだけ直線や平面が平行であるかを表す幾何公差。
・直角度；データム直線またはデータム平面に対して、どれだけ直角から傾いているかを示す幾何公差。記述する数値は、角度ではなく、mm単位で表します。
・傾斜度；データム直線またはデータム平面に対して、どれだけ指定角度（90°を除く）から傾いているかを表す幾何公差。直角度と同様に、角度ではなくmm単位で表します。
・位置度；データムまたは他の形体に関連して定められた点、直線、平面に対して、どれだけ位置ズレしているかの幾何公差。
・同心度；データム円の中心に対して、他の円の中心位置がどれだけズレているかを表す幾何公差。
・同軸度；データム軸直線と同一直線上にあるべき軸線が、どれだけ正確な位置からズレているかを表す幾何公差。
・対称度；データム軸直線またはデータム中心平面に対して、互いに対称であるべき形体がどれだけ正確な位置からズレているかを表す幾何公差。
・円周振れ；データム軸直線を軸とする回転体を回転させたとき、指定した任意の箇所がどれだけズレているかを表す幾何公差。
・全振れ；データム軸直線を軸とする回転体を回転させたとき、その表面がどれだけ振れているかを表す幾何公差。

(参考ブログ)
https://www.pec-kumata.com/post/geometricaltolerance