相関分析について

　生産技術業務の中で頻繁に活用し、知っておくべき統計手法の基本的な内容でもある相関分析について簡単にコメントします。

　相関分析（correlation Analysis）とは、2つ以上の変数間にある関係性を調べるための統計手法です。相関分析を行うことで、2つの変数がどの程度関連しているかを知ることができます。相関分析には、2つの変数間の関係性を示す相関係数が用いられます。

　相関係数は、2 種類のデータの関係を示す指標ですが、相関係数は無単位なので、単位の影響を受けずにデータの関連性を示すことができます。

　相関係数は －1 から 1 までの値を取ります。そして、値が 1 や －1 に近いほど（つまり、絶対値が 1 に近いほど）直線的な相関が強く、0 に近いほど相関が弱いといえます。

　相関係数rを求めるには、共分散をそれぞれの変数の標準偏差で割ります。具体的には、次の公式で計算することができます。
　r=Sxy/SxSy 　 (Sxy;xとyの共分散、Sx;xの標準偏差、Sy;yの標準偏差）

平均値 → 偏差 → 分散 → 標準偏差 → 共分散 の順番で計算することで、相関係数を求めることができます。

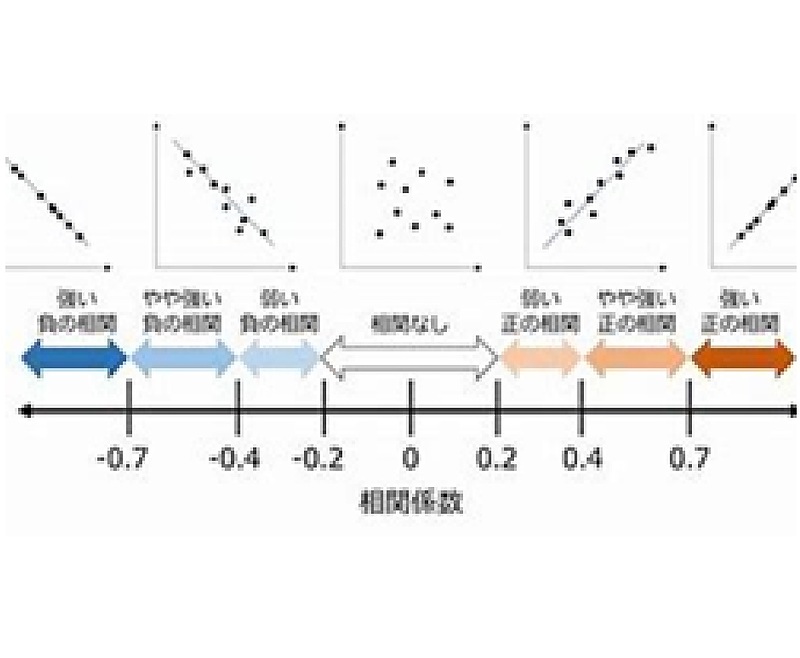
　相関係数は、その相関の強さを-1から1までの数値で表すことができます。
簡単に言うと、
➀-1に近いほど負の相関が強く、
②1に近いほど正の相関が強く、
➂0に近いほど相関が無い、　　　　　　 という3点が重要な考え方です。

さらに相関係数はその絶対値の大きさによって、おおよそ以下の4段階で解釈されることが多いです。
0～0.2：相関が無い
0.2～0.4：弱い相関がある
0.4～0.7：中程度の相関がある
0.7～1：強い相関がある

そのため、たとえ相関係数の符号が正でもその値が小さい場合、そこには相関が無いかもしれないと解釈されます。

(参考ブログ)
https://www.pec-kumata.com/post/correlationanalysis