FEM解析について

　FEMとは、有限要素法 （Finite Element Method）のことですが、様々な物理現象の解析手法として、古くから使われているものです。生産技術分野においても例外ではなく、色々な加工方法に対する理論解析の一つとしてその活用の範囲は大変広く、実験値の裏付け証明や実験そのものの代用として使用されます。
ここでFEMについて簡単に説明します。（一部、ネット情報を引用）

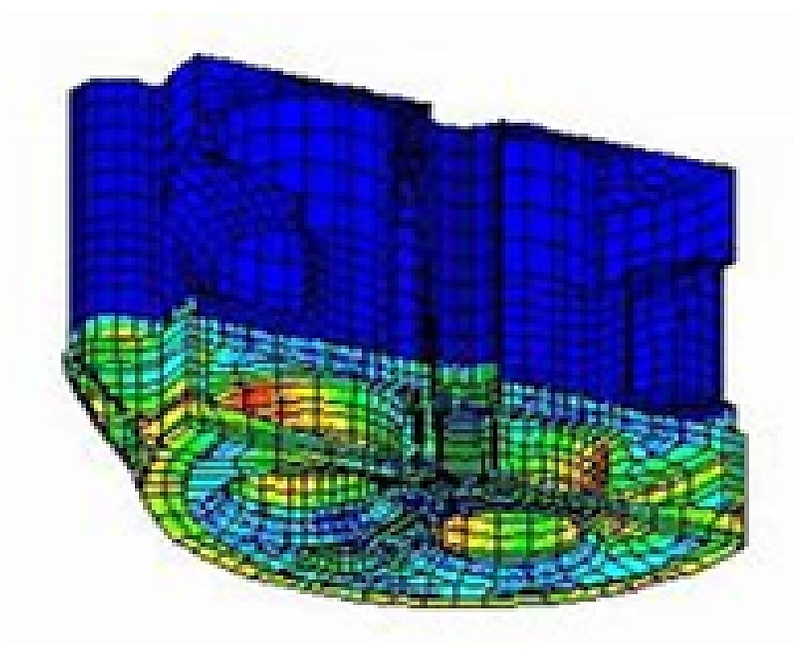
　FEMはコンピュータによって物理シミュレーションを行うための手法の一種であり、連続な物体を有限個の「要素」に分割し、各要素の特性を単純な数学的モデルで近似し、連立方程式の形にして全体の挙動を解析する手法です。

　弾性体の変形問題、熱伝導の問題、流れの問題など、いわゆる連続体の問題は数学的に記述すれば偏微分方程式の問題になるので、それを解くことは容易ではありません。特に構造物が複雑な場合は、極めて困難な問題になります。しかし、物体を細かく分割し個々の小部分だけについて考えるならば、その特性を比較的簡単な式で近似解が得られます。これがFEMの基本的な発想です。

　FEMの数学的理論の誕生は1940年代までさかのぼります。まず欧米の航空工学分野で研究され、その後、土木工学、建築構造工学、機械工学などの分野に広がりました。FEMは大規模なマトリクス(行列)演算を伴うため、コンピューター技術の発達に伴い適応範囲や問題規模は拡大し、現在では工学分野全般で用いられるようになっています。

　FEMの適用範囲を列挙すると下記のようになります。
（1）線形解析
　・線形解析 ・固有値解析 ・座屈固有値解析
（2）非線形解析
　・弾塑性解析 ・クリープ解析 ・超弾性 ・大変形解析
　・各種接触問題 ・非線形動的解析
（3）動的解析
　・過渡応答解析 ・スペクトル応答解析 ・周波数応答解析 ・強制振動問題
（4）熱伝導解析
　・定常、非定常熱伝導解析
　・強制対流、発熱、温度を含む線形、非線形解析
（5）流体解析
（6）電磁場解析
（7）最適化設計

　生産技術に関する、様々な物理現象課題（加工工法検討、機械構造検討、最適条件検討等）に対し、このFEMは有益な手段となります。その検討の方向性に対する支援が生産技術コンサルティング対象となります。

（参考ブログ）
https://www.pec-kumata.com/post/finiteelementmethod