中学数学　超苦手な「三角形の合同証明」を得意にする3つの方法！

こんにちは。

国語専門オンライン学習塾　啓理学舎・代表の篠田です。

今回の話題は、『中学数学　苦手な「三角形の合同証明」を得意にする3つの方法！』です。

当塾は国語専門の学習塾ですが、今回は中学数学で習う「三角形の合同証明」についてコラムを書きます。

なぜ中学数学について書くかは、次項を参照してください！

なぜ国語教師が「三角形の合同証明」のコラムを書くのか？

図形の証明（三角形の合同を含む）は、数学の他の分野と違い、計算をほとんど利用せず、論理的思考力をより必要とする分野です。

そのため、「型」を意識して学ぶととてもわかりやすく、身につきやすい分野です。

当塾では、国語の力は論理的思考力と考えています。

よって、当塾は国語専門の学習塾ですが、「国語」と「図形の証明」は、「論理的思考力」という共通項があるため、このコラムを書いています。

論理的思考力については、こちらのコラムを参照ください。

⒈「定義・定理」「三角形の合同条件」の意味をしっかり理解しよう！

◉「定義・定理」って何？

さて、三角形の合同証明を学ぶときに必ずに出てくる「定義・定理」についてお話をさせていただきます。



定義って、定理って、なんですか？

と言われてもしっかりと意味を言える方は少ないと思います。


ただし、これを知っておくと三角形の合同証明をする上でとても理解力が深まりますので、しっかりと理解してください。

まずは「定義」ですが、


「昔、偉い学者さんたちが決めたこと。」

と考えてください！



たとえば、「2つの辺が等しい三角形を二等辺三角形」としましょうと決めただけです。


別の学者さんたちなら、「2つの辺が等しい三角形を二辺等三角形」と決めたかもしれません。


つまり、「定義とは、決まり・ルール。」なのです。




それでは定理とは何でしょうか？


「定理とは、定義を決めてからわかったこと。」です。



たとえば、「2辺が等しい三角形は二等辺三角形である。」という定義を決めた後、よくよく調べてみたら、


「（二等辺三角形の）2つの底角は等しい。」

「（二等辺三角形の）頂角の二等分線は底辺を垂直に二等分する。」


ということがわかったということです。

まとめると、「定義」を決めた後、よくその図形について調べてわかったことが「定理」なるということです。


◉「三角形の合同条件」って何？


さて、「定義・定理」が理解できたところで、「三角形の合同条件」についてご説明していきます。

まず「合同」の意味ですが、

例えば、紙に書かれている2つの三角形があるとします。

それらをハサミで切り取ります。

そしてその2つの三角形を合わせ、ピッタリと合致したら、「合同」な2つの三角形になります。

言い換えれば、三角形の「形」と「大きさ」がまったく同じなら、「合同」な2つの三角形になります。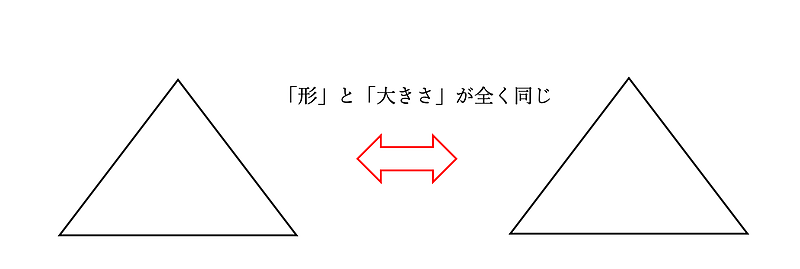



ですから、合同な2つの三角形であるなら、「3つの辺の長さ」と「3つの内角の角度」が一致する（等しい）ことになります。

となると、

2つの三角形が合同かどうかを証明するためには、

2つの三角形の「3つの辺の長さ」と「3つの内角の角度」を調べなければならない？

となります。

もちろんその方法でも合同は証明できます。

しかし、下記のような全部を調べなくても、一部が等しいと分かれば、2つの三角形が合同であるとわかる「三角形の合同条件」というものがあります。

これを利用すれば合同を証明するのが楽になります！

「三角形の合同条件」は以下の3つになります。

○3組の辺がそれぞれ等しい。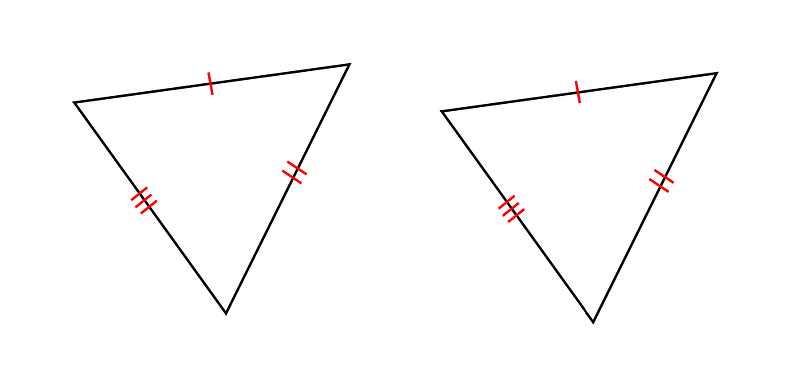

○2組の辺とその間の角がそれぞれ等しい。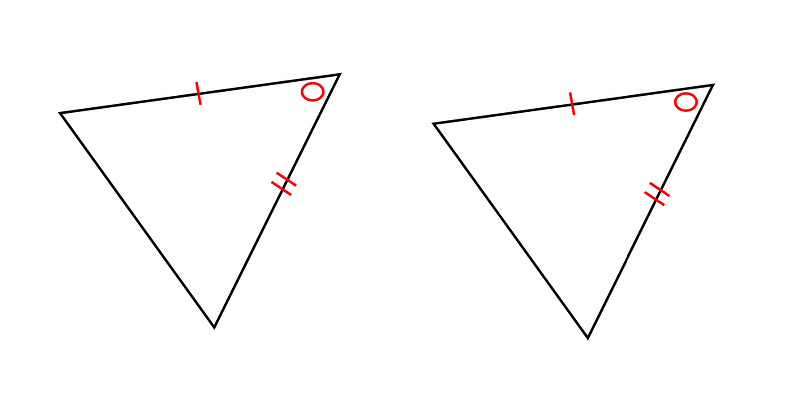

○1組の辺とその両端の角がそれぞれ等しい。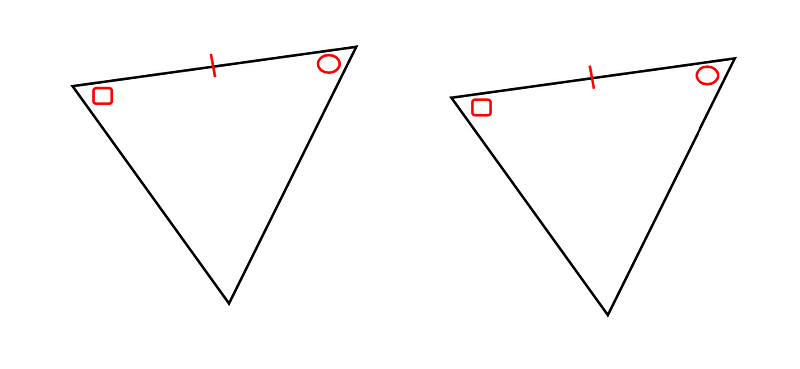


上記の3つの条件のいづれかが当てはまれば、2つの三角形は「合同」ということになります。

⒉「定義・定理」「三角形の合同条件」をしっかり覚えよう！

「定義・定理」「三角形の合同条件」は、国語や英語でいるならば、漢字や英単語にあたります。

漢字や英単語が覚えなければ、文章や英文を読むことはできません！

同じように「定義・定理」「三角形の合同条件」を覚えなければ、図形の証明の問題を解くことはできないしょう！

しっかり、覚えましょう！

覚えておいたほうが良いものを提示しておきます。

（定義・定理集）

覚え方については、いろいろなサイトで紹介されていますので、そちらを参考にしてください！

⒊三角形の合同証明は「型」である！

「定義・定理」「三角形の合同条件」をしっかりと理解し暗記できたところで、実際に証明のやり方について説明させていただきます。

まずは、下記をご覧ください、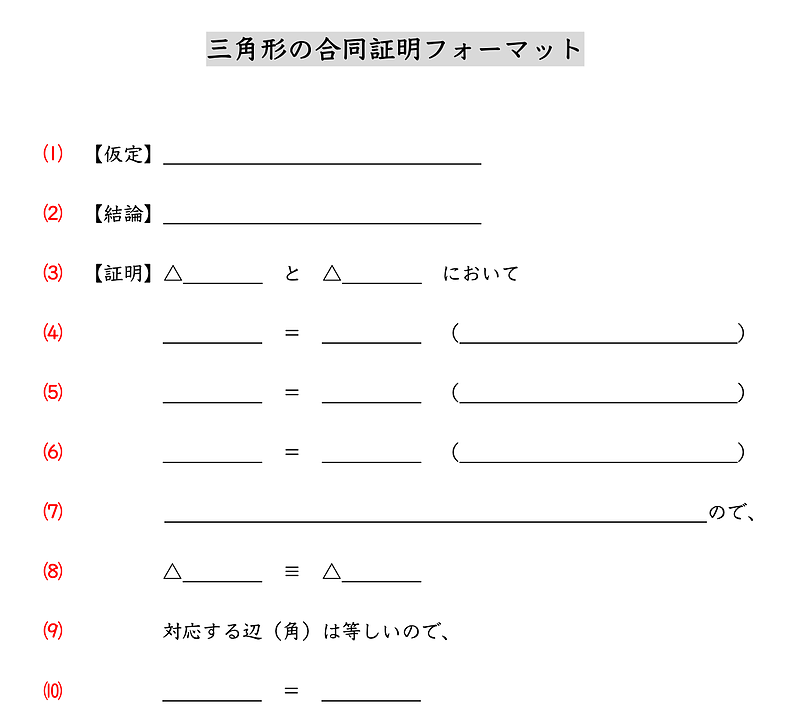


この「三角形の合同証明フォーマット」の「型」を利用すれば、ほとんどの合同証明をすることができます。

つまり、この「型」をマスターすれば、無敵となります。

では、使い方について、お話させていただきます。

◉⑴【仮定】には、問題の前提条件を記入。

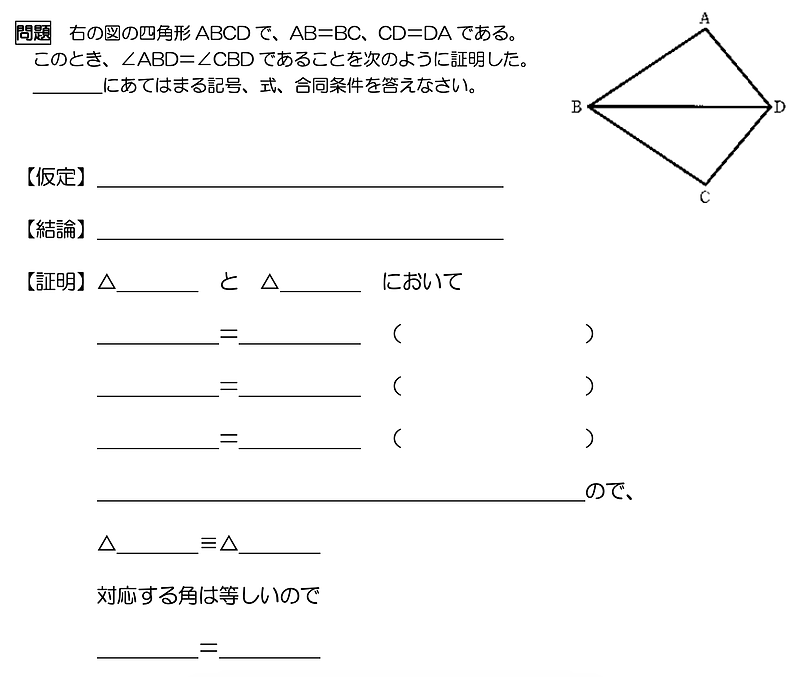
つまり、問題に「○○＝○○である。」等が書かれている場合、それを記入します。

この問題では、問題に「AB＝BC、CD＝DAである。」と書かれているので、【仮定】に「AB＝BC、CD＝DA」と記入します。

◎Checkpoint◎

ここで、「仮定」について少し解説します。

この問題では、「AB＝BC、CD＝DAである。〜であることを次のように証明した。」と書かれていますが、

これはもう少しわかりやすくに書くと、

「仮にAB＝BC、CD＝DAであるならば、〜が等しいことを証明しなさい。」

ということになります。

ですから、「仮定」という言葉を使用しています。

◉⑵【結論】には、証明することを記入。

問題に「∠ABD=∠CBD であることを次のように証明した。」と書かれているので、【結論】に「∠ABD=∠CBD 」と記入します。

◎Checkpoint◎

「結論」とは、「最終的に意見をまとめること」を言います。

ですから、「最終的に証明しなければいけないこと」を記入します。

◉⑶合同を証明する2つの三角形のアルファベットを記入。

ここで注意が必要なのは、アルファベットの順番です。

2つの三角形の対応する頂点順に書いていきます。

例えば、△BDA（≡の左）と記入するなら、△BDC（≡の右）と記入します。

◎Checkpoint◎

ここで疑問に思うことがあるかもしれません。

それは、

「問題は角が等しいことを証明しなさいと言っているのに、なぜ、三角形の合同証明をするのか？」

ということです。

それは、2つの三角形の合同証明を利用して、∠ABD=∠CBDを証明するためです。

つまり、三角形の合同証明すれば対応する辺と角は全て等しくなるため、対応する角である∠ABDと∠CBDは等しいと言えるのです、

◉⑷〜⑹には、等しい辺と角、（　　）の中には等しい理由を記入。

（　　　）の中は、等しい理由を記入します。

⑷と⑸では、等しい辺を2組書いていますが、これらが等しい理由は、問題文に等しいと書かれていたので、「仮定」と記入します。

⑹では、△ABDの（辺）BDと△CBDの（辺）BDが合わさっているため、等しくなります。

そういう場合、「共通」と記入します。

1つの辺が、2つの三角形の一辺になっているということです。

よって、BD＝BD（共通）となります。

◎Checkpoint◎

ここで、注意が必要なことは、2点あります。

1つ目は、

「＝」の左右にどちらの三角形の辺や角を記入するのか？

ということです。

⑶「【証明】△ABDと△CBDにおいて」と記入しているのであれば、⑷「AB＝CB」と書きます。

もし、⑶「【証明】△CBDと△ABDにおいて」と記入しているのであれば、⑷「CB＝AB」と書きます。

つまり、「三角形①と三角形②」と書いているならば、「①の辺＝②の辺」と書くということになります。

2つ目は

また、辺や角のアルファベット順番は？

ということです。

これは、前にも書きましたが、

2つの三角形の対応する頂点順に書いていきます。

例えば、⑷において、＝の左側に「AB」と書くなら、＝の右側に「CB」と書きます。

もし、＝の左側に「BA」と書くなら、＝の右側に「BC」と書きます。

◉⑺は、三角形の合同条件を記入。

この問題では、三角形の合同条件のひとつである「3辺がそれぞれ等しい。」にあたるため、それを記入します。

◉⑻は、どの三角形とどの三角形が合同かを式を使って記入。

ここは、⑶と同じことを記入します。

◉⑼は、問題が問うている、証明するべき、式を記入。

ここは、⑷と同じことを記入しますが、アルファベットの順番に気をつけてください。

なぜなら、⑷は問題文に書かれたものを記入していましたが、ここでは、合同記号（≡）左右、アルファベットの順番に注意してください。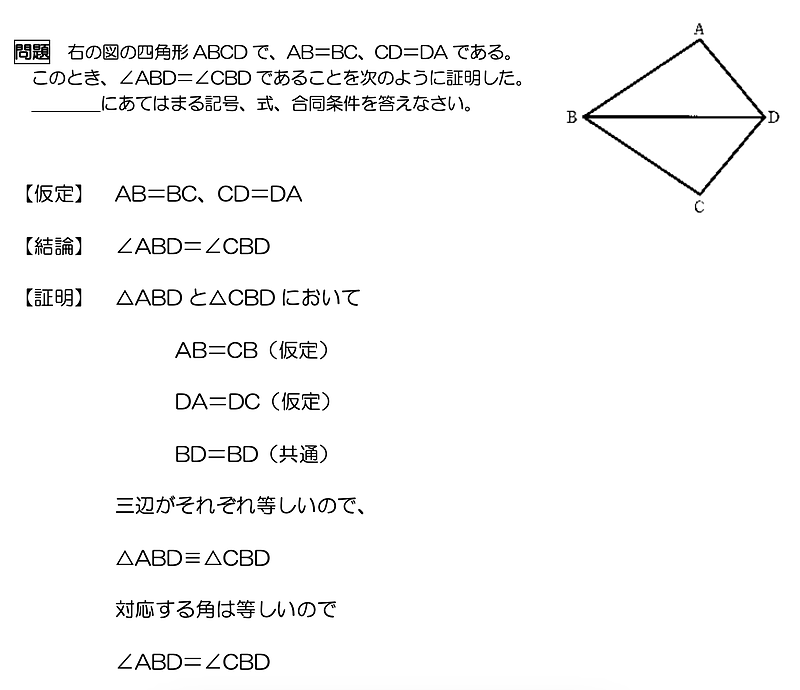

まとめ

まずは、定義、定理の意味をしっかり理解し、それらを覚え、型通りに証明をしていきましょう！

そうすれば、必ず証明が得意になるはずです！

頑張りましょう！


コラム『中学数学　超苦手な「なるため条件」をマスターするたった1つの方法