数学が苦手な中1・中2生をお持ちの保護者様へ 第2回
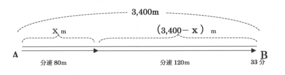
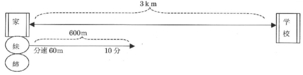
前回は、中学1年で習う「速さの方程式」を取り上げました。今回は「原価・定価・値引き・売価」に関する問題を取り上げたいと思います。良く出題されるパターンを取り上げます。「原価・定価・値引き・売価」に関する問題は中3の二次方程式でも出てまいります。参考にしていただければと思います。
【問題例】
原価に200円の利益を見込んで定価をつけた。売れなかったので定価の1割引で売ったところ50円の利益がでた。原価はいくらか。
【一般的な解き方】
原価をx円とする。
200円の利益を見込んで定価をつけたのだから
定価は(x+200)円。
定価の1割引で売ったのであり1割は0.1だから
1-0.1=0.9で売った事になる、
よって売価は0.9(x+200)となる。
利益は売価―原価だから
0.9(x+200)-xとなり、これが50円だから
0.9(x+200)-x=50
x=1300
答 1300円
中学生がまずつまずきがちなのが、「原価」「利益を見込んで」「定価」「売価」「利益」などの耳慣れない言葉でしょう。商売をした事が無いのですから耳慣れなくて当然なのです。
お子様がこのパターンの問題が分からないとおっしゃった場合は、まず用語の説明からしてあげましょう。お子様がお母様に質問してきたとします。
【説明例】
文房具を売って商売を始めようと思うの。
お母さんがこのボールペン(手近にあるもので結構です)を100円で買ってきました。
これをお店において、300円で売る事にして値札を「300円」とつけました。
この300円が定価だね。もし定価で売れたとしたら、お母さんは200円儲かるよね。
これが「200円の利益を見込んで定価をつける」という事だよ。
「300円」と値札をつけたこのボールペン、300円で売れるかな?
うーーん、残念な事に売れなかったんだよ。高すぎたのかな?
それで値引をする事にしました。いくらなら売れるかな?
思い切って120円、値引しました。そうすると売れました。
定価300円のものを120円値引したら、いくらで売れたことになるかな?
そう、300円から120円を引いて180円で売れたことになるね。
この180円が「売価」だよ。
じゃあ、お母さんはいくら儲かったでしょう。
もともと100円で買ったきたものを180円で売ったのだから、儲かったのは80円だね。これが利益だよ。
ここで注目してね。80円はどうやって計算したかというと、売価の180円から原価の100円を引いたよね。これを覚えておいて。売価から原価を引いたのが利益だよ。
これを図にすると下のようになるね。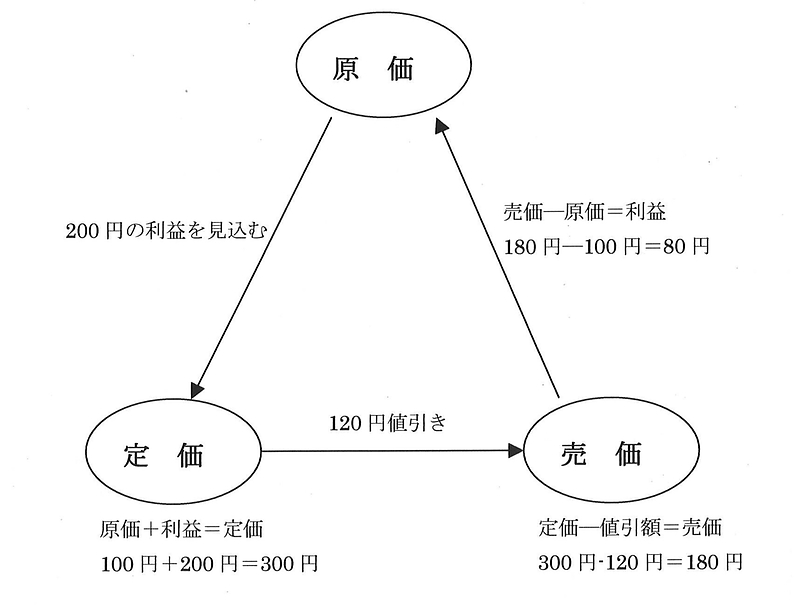
180円で売れなかった時の事も考えておこうね。仕方ないからもっと値引して50円でやっと売れたとしよう。そうすると売価が50円だね。売価から原価を引くと、50-100=-50となるね。売価から原価を引いて-になったら、これを損失と言うんだよ。覚えておくといいね。
じゃあ、最初の問題を図を使ってといてみようか。
その時に公式を覚えておこう。次の2つだよ。
①割引=もと×(1―割引分)
②割増=もと×(1+割増分)
原価をx円とするね。図に書き込んでみよう。
200円の利益を見込むと定価はx+200になるね。これも書き込んでおこう。
次に「定価の1割引で売った」とあるね。1割引をした「もと」はなんだろう。
そう、定価だね。だから①の公式に当てはめて
(x+200)×(1-0.1) になるね。1-0.1=0.9だからこの式は
定価 1割引
0.9(x+200)という事になるね。これが売価だよ。図に書き込んでおこう。
最後に50円の利益が出たと書いてあるね。
利益の計算は、売価―原価だったよね。
じゃあ、やってみよう。
0.9(x+200)-x =50
売価 原価 利益
これがxを求める式になるね。
計算するとx=1300 答 1300円
図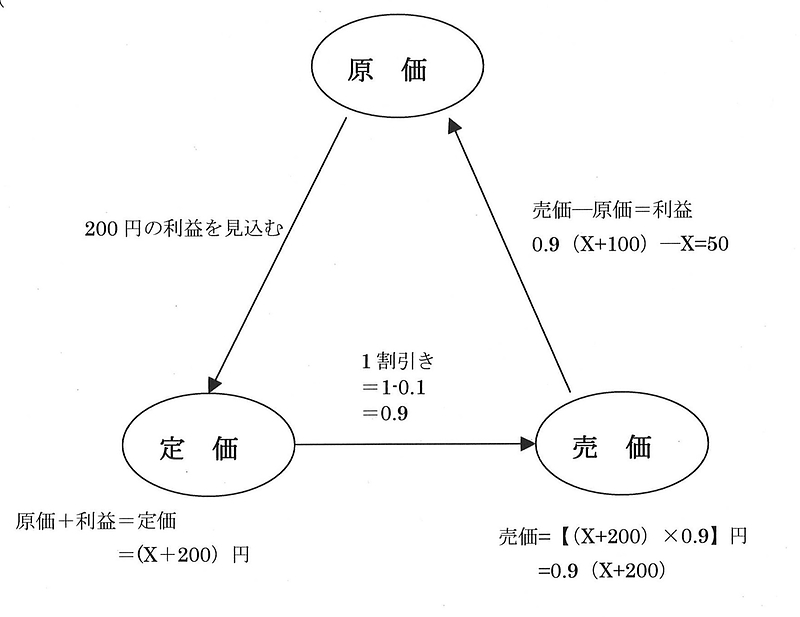
最後に、お子様に説明してあげる時の「コツ」を申し上げます。
塾の講師が良く使う手です。
今回のような少しややこしい説明の場合は、説明を必ず2回繰り返してあげてください。
1回目は懇切丁寧に説明してあげてください。2回目はさらっと、ポイントを抑える程度に説明してあげてください。
説明を2回繰り返す事で、説明を受ける側は「よく分かった」という印象をもちます。1回目の懇切丁寧な説明の際に聞き漏らした事も、2回目の説明で確認する事が出来ます。
2回説明を繰り返す事でお子様の理解度、定着度は確実に上がります。試してみてください。