数学の苦手な中学生をお持ちの保護者様へ

前回は、「小6からの中学入試」として、塾との協力関係ついてお話しました。
今回は話題を変えて、数学の苦手な中学生のお子様をお持ちのお母様、お父様に入試での頻出単元をいくつかピックアップして、苦手克服の仕方についてお話したいと思います。

今回は、中学1年で習う「速さの方程式」を取り上げます。
＜問題例＞
A地点からB地点まで3400mあります。花子さんはA地点を出発してはじめは分速80mで歩き、途中から分速120mで歩きました。A地点を出発してからB地点に付くまで33分かかりました。分速80mで歩いた距離は何mでしょう。
＜図＞
分速80mで歩いた距離をxmとします。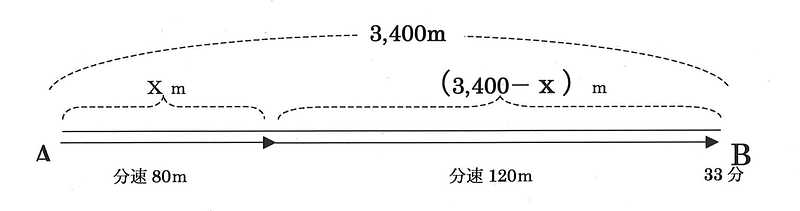



上のような図は教科書や参考書に書いてあります。
速さの問題ではよく、距離＝速さ×時間、時間＝距離/速さ、速さ＝距離/時間などの公式を使います。
　
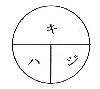　という図をご覧になったことのある方もいらっしゃると思います。

上の問題では、距離がx、3400－x、速さが80、120、時間が33なので
x/80+（3400－x）/120＝33　
というような式になるでしょう。このパターンの式も教科書や参考書に書いてあります。

数学の苦手な生徒が教科書や参考書の解説を見ても速さの問題を解く事が出来ないのは何故でしょう。
私が中学生を受け持っていた頃、中3生で受験前になっても、どうしても速さの文章題を正解できない生徒がいましたので、補習をしました。
私が補習した生徒は「えー、分速80mって、距離じゃないの？私、これが距離だと思ってたー！！だって80mって書いてるもん」と言いました。
決して出来ない生徒ではありません。むしろ中学では上位の成績を取っている生徒です。しかし一度思い違いをすると、ずっとそのまま思い込み、さらにいまさら聞くことも出来ないのでそのまま不正解を続けて、「自分は速さが苦手なんだ」と思い込みます。
速さの問題がどうしても正解できないお子様には第1段階として、どれが距離でどれが速さなのかはっきりと分かるようにアドバイスをしてあげてください。

次に問題は、x/80+（3400－x）/120＝33　からの計算です。
テキストによってはいきなりx=1120と答えが書いてある場合があります。
「何故、1120になるの？」と戸惑っている生徒もいるでしょう。

分母の80と120を消すために両辺に240をかける、という説明が一般的ですが、生徒が間違いやすい例が下記になります。
誤：3x+6800-x=7920
誤：3x+6800-2x=33
計算間違いをしている場合は、計算過程として
3x+2(3400-x)=33×240
3x+6800-2x=7920
3x-2x=7920-6800
x=1120
ここまで説明してあげていただきたいと思います。

次回は「速さの方程式」第2弾として、別のパターンの問題を取り上げたいと思います。

＜お知らせ＞
①京進からのお知らせ
京進HP

②さらに広く学習相談を受け付けるため、学習相談専用のフリーダイヤルを開設しました。
京進これから研究所内「江川先生の学習相談ダイヤル」：0120－770－878
すでにお子様の学習相談や受験についてのご相談電話を多数いただいております。
電話受け付け：祝日を除く、火・金の13：00～18：00
お子様の勉強についてお気軽にご相談いただければと思います。

（京進これから研究所とは？）
京進これから研究所では、将来にわたって生徒さんに役立つ何かを提供できるように教育企業としてできることを日々研究しています。新規事業の種（シーズ）の収集や新商品の開発、教育指導方法、生徒さんのやる気向上の問題などを研究しております。