複利と単利について

お客さまにお伝えしたいこと

• 利回りには「単利」と「複利」があり、資産運用においては「複利」で運用することによる「複利効果」で資産の成長が期待できる

• 資産運用の目安として「72の法則」「115の法則」を知っておくと便利

　資産運用の際に耳にする「利回り」には、「複利」と「単利」の2種類があります。どちらも運用の成果を示すものですが、利回りの受け取り方によって最終的な資産成長の仕方が変わっていきます。

　「単利」とは運用する元本に対しての利回りです。単利を計算式で表すと「元本×利回り」となり、常に同じ元本から発生する利回りを受け取る仕組みとなります。
　それに対して、「複利」は運用する元本にそれまでに受け取った利益を組み入れた合計に対する利回りです。したがって、各期の利益が次第に増加していき、雪だるま式に利益が積み上がっていく仕組みとなります。

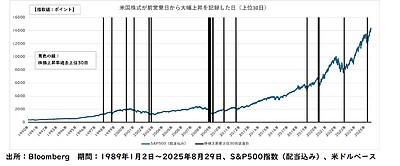
　そのため、長期間運用する際には「複利」で運用する方が将来の資産がより大きく成長していきます。　
　1000万円を年率5％で運用した場合、税金等を考慮しなければ、単利での運用では毎年50万円ずつ利益を受け取ります。
5年間では1000万円に5年分の250万円を加えた1250万円が運用総額となります。
　一方で、複利での運用では、毎年の利益を1000万円に加えて運用していくので、同様に5年運用した場合の運用総額は約1,276万円となり、単利よりも約26万円多くなります。
　この複利による上乗せ分は「複利効果」と呼ばれており、資産運用において長期継続して運用することのメリットとなっています。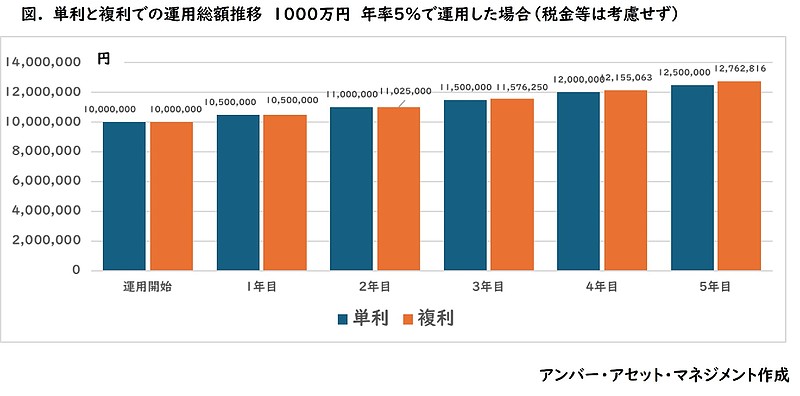

　更に運用する期間が長くなるほど、複利効果が大きく発揮されます。年率5％の運用で30年運用すると単利の2500万円に対して複利は約4322万円と約1.7倍もの差を生み出します。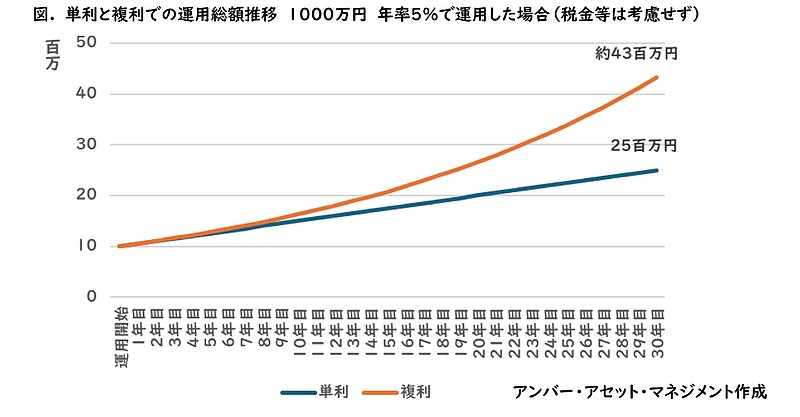


　また、「複利効果」をより分かり易くイメージするのに「72の法則」「115の法則」が役に立ちます。

これは、資産を2倍又は3倍にするには何年かかるかを簡易的に計算するもので、計算式は以下の通りです。

　　72 ÷ 年利回り ＝ 資産が2倍になる年数(※近似値)
　 115 ÷ 年利回り ＝ 資産が3倍になる年数(※近似値)

例えば、年率の利回り7％で運用した場合、資産を2倍にするには72 ÷ 7％ ＝ 約10.2年かかるという計算になります。利回りが高くなるに従って、資産が2倍になるために必要な年数が短くなっていきます。

ちなみに、一般的な10年定期預金の金利に近い0.2％で運用すると、資産を2倍にするのに必要な年数は約360年と膨大な時間を要するのが分かります。

お客さまの人生計画に沿って、どのぐらいの利回り、運用期間であれば目標とする運用資産額に届きそうか、大まかな　目安として、「72の法則」や「115の法則」を知っておくと便利だと思います。


【関連動画】複利のチカラ